ON ZERO DIVISOR GRAPH OF MATRIX RING 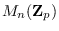$M_n(\mathbf{Z}_p)$
Vijay Kumar Bhat1, Pradeep Singh2
1,2 School of Mathematics
SMVD University
Katra - 182320, INDIA

Abstract

Consider $M_n(\mathbf{Z}_p)$, the matrix ring of order $n$ over the field $\mathbf{Z}_p$. In this paper, we deduce a relation to find the number of zero divisors in matrix ring $M_{n}(\mathbf{Z}_p)$. We prove that zero divisor graph of $M_2(\mathbf{Z}_p)$ is a regular directed graph. We also prove that the diameter of zero divisor graph of $M_n(\mathbf{Z}_p)$ is 2.

Citation details of the article



Journal: International Journal of Applied Mathematics
Journal ISSN (Print): ISSN 1311-1728
Journal ISSN (Electronic): ISSN 1314-8060
Volume: 34
Issue: 6
Year: 2021

DOI: 10.12732/ijam.v34i6.5

Download Section



Download the full text of article from here.

You will need Adobe Acrobat reader. For more information and free download of the reader, please follow this link.

References

  1. [1] D. F. Anderson and A. Badawi, The total graph of a commutative ring, J. Algebra, 320 (2008), 2706-2719.
  2. [2] D. F. Anderson and P. S. Livingston, The zero-divisor graph of a commutative ring, J. Algebra, 217 (1999), 434-447.
  3. [3] I. Beck, Coloring of commutative rings, J. Algebra, 116 (1988), 208-226.
  4. [4] I. Boˇzi´c and Z. Petrovi´c, Zero-divisor graphs of matrices over commutative rings, Comm. Algebra, 37 (2009), 1186-1192.
  5. [5] J. Warfel, Zero-divisor graphs for direct products of commutative rings, Wabash College Technical Reports, 2 (2004).
  6. [6] L. Birch, J. Thibodeaux and R. Tucci, Zero divisor graphs of finite direct products of finite rings, Comm. Algebra, 42 (2014), 3852-3860.
  7. [7] M. Axtell and J. Stickles, Zero-divisor graph of idealizations,J. Pure Appl. Algebra, 204 (2006), 235-243.
  8. [8] S. Akbari and A. Mohammadian, On the zero-divisor graph of noncommutative ring, J. Algebra, 296 (2006), 462-479.
  9. [9] R. Farooq and M. A. Malik, On some eccentricity based topological indices of nanostar dendrimers, Optoelectronics and Advanced MaterialsRapid Communications, 9 (2015), 842-849.
  10. [10] P. A. Krylov, A. V. Mikhalev and A. A. Tuganbaev, Endomorphism ring of abelian groups. J. Math. Sci., 110 (2002), 2683-2745.
  11. [11] S. P. Redmond, The zero-divisor graph of a non-commutative ring, Internat. J. Commutative Rings, 1 (2002), 203-211.
  12. [12] S. P. Redmond Structure in the zero-divisor graph of a non-commutative ring, Houston J. Math., 30 (2004), 345-355.
  13. [13] S. Safaeeyan, E. Momtahan and M. Baziar, A generalization of the zerodivisor graph for modules, J. Korean Math. Soc., 51 (2014), 87-98.
  14. [14] V. Sharma, R. Goswami, and A. K. Madan, Eccentric connectivity index: a novel highly discriminating topological descriptor for structure-property and structure-activity studies, J. Chem. Inf. Comp. Sci., 37 (1997), 273- 282.
  15. [15] P. Singh, and V. K. Bhat, Zero-divisor graphs of finite commutative rings: A survey, Surv. Math. its Appl., 15 (2020), 371-397.
  16. [16] P. Singh, and V. K. Bhat, Adjacency matrix and wiener index of zero divisor graph (Zn), J. Appl. Math. Comput., 66 (2021), 717-732; doi: 10.1007/s12190-020-01460-2.
  17. [17] P. Singh, and V. K. Bhat, Graph invariants of the line graph of zero divisor graph of Zn,J. Appl. Math. Comput.; doi: 10.1007/s12190-021-01567-0.
  18. [18] X. Ma, D. Wang and J. Zhou, Automorphisms of the zero-divisor graph over 2 × 2, J. Korean Math. Soc., 53 (2016), 519-532.