A UNIFORM ABSOLUTE CONTINUITY OF
INTEGRAL RESULT IN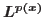 $L^{p\left(x\right)}$
Yasin Kaya
Department of Mathematics
Faculty of Education
Dicle University
Diyarbakır - 21280, TURKEY

Abstract

In this paper we prove a uniform absolute continuity of integral result in variable exponent Lebesgue space. The idea of our proof is similar to that for the classical Lebesgue space.

Citation details of the article



Journal: International Journal of Applied Mathematics
Journal ISSN (Print): ISSN 1311-1728
Journal ISSN (Electronic): ISSN 1314-8060
Volume: 30
Issue: 5
Year: 2017

DOI: 10.12732/ijam.v30i5.6

Download Section



Download the full text of article from here.

You will need Adobe Acrobat reader. For more information and free download of the reader, please follow this link.

References

  1. [1] D. Cruz-Uribe, A. Fiorenza, Variable Lebesgue Spaces: Foundations and Harmonic Analysis, Springer Science & Business Media (2013).
  2. [2] L. Diening, P. Harjulehto, P. Hästö, and M. Růžička, Lebesgue and Sobolev Spaces with Variable Exponents, Lecture Notes in Mathematics, Vol. 2017, Springer, Berlin (2011).
  3. [3] O. Kováčik, J. Rákosnı́k, On spaces Lp(x) and W 1,p(x) , Czechoslovak Math. J., 41, No 4 (1991), 592-618.
  4. [4] X. Fan, D. Zhao, On the spaces Lp(x) and W m,p(x) , J. Math. Anal. Appl., 263, No 2 (2001), 424-446.
  5. [5] W. Orlicz, Über konjugierte exponentenfolgen, Studia Math., 3, No 1 (1931), 200-211.