BLOW-UP TIME OF SOLUTIONS FOR
SOME NONLINEAR PARABOLIC EQUATIONS
SOME NONLINEAR PARABOLIC EQUATIONS
Abstract. In this paper, we consider the following initial-boundary value
problem

where ,
,
 ,
,
 for
for  ,
,  is a positive
parameter,
is a positive
parameter, 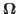 is a bounded domain in
is a bounded domain in
 with
smooth boundary
with
smooth boundary
 ,
, 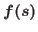 is positive,
nondecreasing, convex function for positive values of
is positive,
nondecreasing, convex function for positive values of  and
and
 . We show that if
. We show that if
 is small enough, the solution
is small enough, the solution  of the above
problem blows up in a finite time and its blow-up time tends to
the one of the solution of the following differential equation
of the above
problem blows up in a finite time and its blow-up time tends to
the one of the solution of the following differential equation
![\begin{displaymath}%\\
\left\{%
\begin{array}{ll}
\hbox{$\alpha^{'}(t)=b(t)f...
...} \\ [4pt]
\hbox{$\alpha(0)=M$,} %\\
\end{array}%
\right.
\end{displaymath}](img18.png)
as goes to zero, where
goes to zero, where
 .
.

where
![\begin{displaymath}%\\
\left\{%
\begin{array}{ll}
\hbox{$\alpha^{'}(t)=b(t)f...
...} \\ [4pt]
\hbox{$\alpha(0)=M$,} %\\
\end{array}%
\right.
\end{displaymath}](img18.png)
as
Finally, we give some numerical results to illustrate our analysis.
AMS Subject Classification: 35B40, 35B50, 35K60, 65M06
Key Words and Phrases: blow-up, nonlinear parabolic equation, numerical blow-up time, finite difference, convergence
Download full article from here (pdf format).
DOI: 10.12732/ijam.v29i1.4
Volume: 29
Issue: 1
Year: 2016

