THE HARMONIC ANALYSIS ASSOCIATED TO
THE CHEREDNIK-TRIMÈCHE'S
TRANSMUTATION OPERATORS ON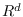 $\mathbb{R}^d$
Khalifa Trimèche
Faculty of Sciences of Tunis
Department of Mathematics
CAMPUS, 2092 Tunis, TUNISIA

Abstract

We consider in this paper two Cherednik operators $T^k_j, T_j^l$, $j=1,2,3,...,d,$ on $\mathbb{R}^d$, associated to the multiplicity functions $k,l$. First we define and study in this paper the Cherednik-Trimèche's transmutation operator $U_{kl}$ and its dual $^{t}U_{kl}$. Next we study the Harmonic Analysis associated to these operators.

Citation details of the article



Journal: International Journal of Applied Mathematics
Journal ISSN (Print): ISSN 1311-1728
Journal ISSN (Electronic): ISSN 1314-8060
Volume: 31
Issue: 6
Year: 2018

DOI: 10.12732/ijam.v31i6.2

Download Section



Download the full text of article from here.

You will need Adobe Acrobat reader. For more information and free download of the reader, please follow this link.

References

  1. [1] I. Cherednik, A unification of Knizhnik-Zamolod-dchnikov equations and Dunkl operators via affine Hecke algebras, Invent. Math. Res., 106 (1991), 411-432.
  2. [2] G.J. Heckman, E.M. Opdam, Root systems and hypergeometric functions I, Compositio Math., 64 (1987), 329-352.
  3. [3] E.M. Opdam, Harmonic analysis for certain representations of graded Hecke algebras, Acta Math., 175 (1995), 75-121.
  4. [4] B. Schapira, Contribution to the hypergeometric function theory of Heckman and Opdam; sharp estimates, Schwartz spaces, heat kernel, Geom. Funct. Anal., 18 (2008), 222-250.
  5. [5] K. Trim`eche, The trigonometric Dunkl intertwining operator and its dual associated with the Cherednik operators and the Heckman Opdam theory, Adv. Pure Appl. Math., 1 (2010), 293-323.
  6. [6] K. Trim`eche, Harmonic analysis associated with the Cherednik operators and the Heckman-Opdam theory, Adv. Pure Appl. Math., 2 (2011), 23-46.
  7. [7] K. Trim`eche, The positivity of the hypergeometric translation operators associated to the Cherednik operators and the Heckman-Opdam theory attached to the root system of type BC2, International Journal of Applied Mathematics, 29, No 6 (2016), 687-715; doi: 10.12732/ijam.v29i6.4; available at: http://www.diogenes.bg/ijam/index.html.