IJAM: Volume 29, No. 3 (2016)

Abstract. In this paper we study the linear stability of the displacement of a Newtonian fluid by air in a 3D Hele-Shaw cell. We obtain a new formula of the growth constant , containing two new terms, compared with the Saffman-Taylor formula. We get two new results: a) the displacement is almost stable even if the displacing fluid is less viscous but the surface tension 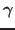on the air-fluid interface is large enough; b) if 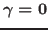, then is bounded in terms of the wavenumber 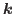and tends to zero for very large 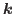. The above new results are in contradiction with the classical Saffman-Taylor criterion for the stability of 2D immiscible displacement in Hele-Shaw cells.