LOCAL WELL-POSEDNESS OF THE REGULARIZED
rBO-ZK EQUATION IN SOBOLEV SPACES
OF NEGATIVE INDICES
rBO-ZK EQUATION IN SOBOLEV SPACES
OF NEGATIVE INDICES
Abstract. In this paper, we study the local well-posedness of the regularized rBO-ZK equation, defined by

where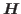 is the Hilbert transform with respect to
is the Hilbert transform with respect to 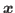 and
and 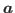 ,
,  ,
,  and
and 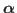 are real numbers, with
are real numbers, with  ,
,  and
and
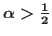 , We show that the associated Cauchy problem is locally well posed in Sobolev space
, We show that the associated Cauchy problem is locally well posed in Sobolev space 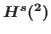 for
for  .
.
where
AMS Subject classification: 35A01, 35G25, 42B35
Keywords and phrases: regularized Benjamin-Ono-Zakharov-Kuznetsov equation, Cauchy problem, negative indices, global and local well-posedness
Download full article from here (pdf format).
DOI: 10.12732/ijam.v28i4.7
Volume: 28
Issue: 4
Year: 2015

