A SUBDIVISION ALGORITHM FOR 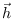$\vec h$-BÉZIER VOLUMES
USING TRIVARIATE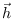 $\vec h$-BLOSSOMING
Ilija Jegdić
Department of Mathematics
Texas Southern University
Houston, TX 77004, USA

Abstract

We extend the definition of $h$-blossoming, introduced by Simeonov, Zafiris, and Goldman, to the trivariate polynomials and we define the $\vec h$- Bézier volumes. We derive a subdivision algorithm for $\vec h$-Bézier volumes and illustrate it on examples using Mathematica.

Citation details of the article



Journal: International Journal of Applied Mathematics
Journal ISSN (Print): ISSN 1311-1728
Journal ISSN (Electronic): ISSN 1314-8060
Volume: 31
Issue: 6
Year: 2018

DOI: 10.12732/ijam.v31i6.6

Download Section



Download the full text of article from here.

You will need Adobe Acrobat reader. For more information and free download of the reader, please follow this link.

References

  1. [1] R. Farouki, The Bernstein polynomial basis: a centennial retrospective, Computer Aided Geometric Design, 29 (2012), 379-419.
  2. [2] R. Goldman, P´olya’s urn model and computer aided geometric design, SIAM J. Alg. Disc. Meth., 6 (1985), 1-28.
  3. [3] R. Goldman, Pyramid Algorithms, A Dynamic Programming Approach to Curves and Surfaces for Geometric Modeling, The Morgan Kaufman Ser. in Computer Graphics and Geometric Modeling, Elsevier Science (2003).
  4. [4] R. Goldman, P. Barry, Shape parameter deletion for P´olya curves, Numer. Algorithms, 1 (1991), 121-137.
  5. [5] I. Jegdi´c, Algorithms and identities for bivariate (h1, h2)blossoming, International Journal of Applied Mathematics, 30, No 4 (2017), 321-343; doi: 10.12732/ijam.v30i4.5; available at: http://www.diogenes.bg/ijam/index.html.
  6. [6] I. Jegdi´c, J. Larson, P. Simeonov, Algorithms and identities for (q, h)Bernstein polynomials and (q, h)-B´ezier curves – a non-blossoming approach, Analysis in Theory and Applications, 32 (2016), 373-386.
  7. [7] H. Oru¸c, G. M. Phillips, A generalization of the Bernstein polynomials, Proc. Edinb. Math. Soc., 42 (1999), 403-413.
  8. [8] H. Oru¸c, G. M. Phillips, q-Bernstein polynomials and B´ezier curves, J. Comput. Appl. Math., 151 (2003), 1-12.
  9. [9] G.M. Phillips, A de Casteljau algorithm for generalized Bernstein polynomials, BIT, 37 (1997), 232-236.
  10. [10] G.M. Phillips, Bernstein polynomials based on q-integers, Ann. Numer. Math., 4 (1997), 511-518.
  11. [11] G.M. Phillips, A survey on the q-Bernstein polynomials, IMA J. Numer. Anal., 30 (2010), 277-288.
  12. [12] M. Samuelˇc´ık, B´ezier and B-spline Volumes, Project of Dissertation, Comenius University, Bratislava, Slovakia (2005).
  13. [13] P. Simeonov, V. Zafiris, R. Goldman, h-Blossoming: A new approach to algorithms and identities for h-Bernstein bases and h-B´ezier curves, Computer Aided Geometric Design, 28 (2011), 549-565.
  14. [14] P. Simeonov, V. Zafiris, R. Goldman, q-Blossoming: A New Approach to Algorithms and Identities for q-Bernstein Bases and q-B´ezier Curves, J. Approx. Theory, 164(1) (2012), 77-104.
  15. [15] D. Stancu, Approximations of functions by a new class of linear polynomial operators, Rev. Roumanie Math. Pures Appl., 13 (1968), 1173-1194.
  16. [16] D. Stancu, Generalized Bernstein approximating operators, Itinerant Seminar on Functional Equations, Approximations and Convexity, ClujNapoca (1984), 185-192.