ON THE GEOMETRY OF CLOSED TIMELIKE
RULED SURFACES IN DUAL LORENTZIAN SPACE
RULED SURFACES IN DUAL LORENTZIAN SPACE
Abstract. In this paper, a dual timelike curve  which is a Lorentzian spherical indicatrix of a timelike closed ruled surface
which is a Lorentzian spherical indicatrix of a timelike closed ruled surface
 with a real parameter
with a real parameter
 , two frames
, two frames
 related to the timelike closed ruled surface
related to the timelike closed ruled surface
 and
and
 which moves respect to
which moves respect to 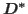 and related to a timelike closed ruled surface
drawn by a timelike vector
and related to a timelike closed ruled surface
drawn by a timelike vector
 , and a timelike vector
, and a timelike vector
 which is fixed in the frame
which is fixed in the frame  are considered;
and dual integral invariants of the timelike closed ruled surfaces which
correspond to the dual timelike closed curves drawn by the vectors
are considered;
and dual integral invariants of the timelike closed ruled surfaces which
correspond to the dual timelike closed curves drawn by the vectors
 and
and
 are studied; and it is found same
relations among the dual integral invariants of the timelike closed ruled
surfaces which correspond to the dual timelike closed curves drawn by the timelike vectors
are studied; and it is found same
relations among the dual integral invariants of the timelike closed ruled
surfaces which correspond to the dual timelike closed curves drawn by the timelike vectors
 and
and
 . In addition, these results are carried
to the Lorentzian line space
. In addition, these results are carried
to the Lorentzian line space
 and give some theorems by
means of Study's mapping.
and give some theorems by
means of Study's mapping.
AMS Subject Classification: 53A17, 53B30
Key Words and Phrases: integral invariants, ruled surface, dual spherical motion
Download full article from here (pdf format).
DOI: 10.12732/ijam.v29i1.2
Volume: 29
Issue: 1
Year: 2016

