THE NON-COMPACTNESS EMBEDDINGS OF
THE RADIAL SOBOLEV SPACES Hr1(Rn)
Richard A. De la Cruz Guerrero1, Juan Carlos Juajibioy2, Leonardo Rendón3
1School of Mathematics and Statistics
Universidad Pedagógica y Tecnológica de Colombia
Av. Central del Norte 39-115
Edificio de Matemáticas, Oficina M202, Tunja, COLOMBIA
2Department of Naturals and Exacts Science
Fundación Universidad Autonoma de Colombia
Calle 12B No. 4-31, Bloque 6, Oficina 211, Bogotá, D.C., COLOMBIA
3Department of Mathematics
Universidad Nacional de Colombia
Kra. 30 No. 45-03, Edificio 405, Oficina 324, Bogotá, D.C., COLOMBIA
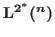Abstract. The purpose of this paper is to give an elementary demonstration on the non-compactness embedding of radial Sobolev spaces $\mathrm{H}_r^1(\mathbb{R}^n)$ in $\mathrm{L}^2(\RR^n)$ and $\mathrm{L}^{2^*}(\RR^n)$ where $2^*=\frac{2n}{n-2}$, $n>2$. First we will show that the embedding $\mathrm{H}_r^1(\mathbb{R}^n)\rightarrow \mathrm{L}^{q}(\mathbb{R}^n)$ is compact for $2<q<2^{*}$, and then we give two examples for the critic cases $q=2$ and $q=2^{*}$ in which the compactness fails.
AMS Subject classification: 35J05, 35J60, 46E35
Keywords and phrases: radial Sobolev space, (non)compact embedding, 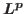$L^p$ spaces, $p$-Laplacian operator


Download full article from here (pdf format).

DOI: 10.12732/ijam.v27i2.7

Volume: 27
Issue: 2
Year: 2014