SINGULAR VALUES AND FIXED POINTS OF
FAMILY OF FUNCTION z ez/(ez-1)
Mohammad Sajid
College of Engineering
Qassim University
Buraidah, Al-Qassim, SAUDI ARABIA
Abstract. The aim of this paper is to study the singular values and fixed points of one parameter family of generating function, $h_\lambda(z)=\lambda \frac{z e^{z}}{e^{z}-1}$, $\lambda \in \mathbb{R} \backslash \{0\}$, which arises from the generalized Bernoulli generating function, Apostol-Bernoulli generating function or Stirling generating function. It is found that the function $h_{\lambda}(z)$ has infinitely many singular values. Further, it is shown that all the critical values of $h_{\lambda}(z)$ are lying outside the open disk centered at origin and having radius $\lambda$. 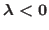Moreover, the real fixed points of $h_{\lambda}(z)$ for $\lambda<0$ and their nature are investigated. 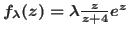Finally, the results found here are compared with the dynamical properties of functions $\lambda \tan z$, $E_{\lambda}(z) = \lambda \frac{e^{z} -1}{z}$ and $f_{\lambda}(z)=\lambda\frac{z}{z+4}e^{z}$ for $\lambda>0$.
AMS Subject classification: 30D05, 37C25, 58K05
Keywords and phrases: fixed points, critical values, singular values


Download full article from here (pdf format).

DOI: 10.12732/ijam.v27i2.4

Volume: 27
Issue: 2
Year: 2014